INTRODUCTION
For a long time robots were confined to industrial tasks that are well defined and very static. Currently we have a large push to move robots to human environments, which means there is the need for interaction either with humans or with other robots. This can be as kitchen aids, in elderly care or to drive us around. These environments can be very dynamic or even chaotic. So there is a lot of added complexity. To tackle that we introduce different abstraction layers that allow a more precise reasoning on a semantic level. The issue with that are different mathemetical representations that reintroduce complexity or unreliability when we need to convert between representations. Many problems in robotics are fundamentally problems of geometry, so choosing a represention with a strong geometrical and physical meaning. Geometric algebra is such a a unified mathematical representation.
SOFTWARE
PUBLICATIONS
Cooperative Geometric Primitives for Multi-Arm Manipulation Control
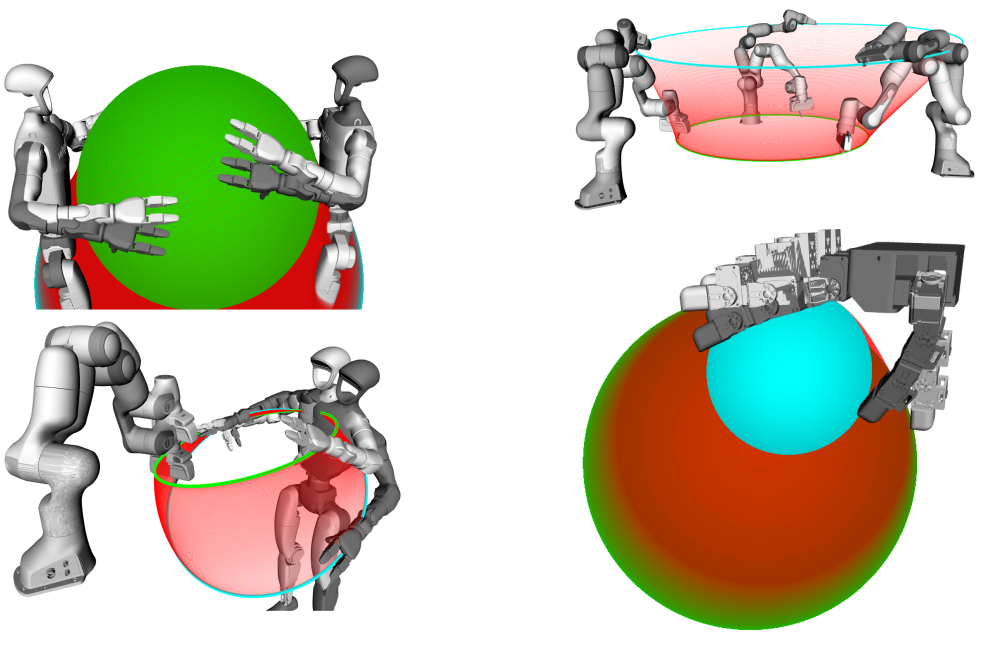
Many tasks in human environments require collaborative behavior between multiple kinematic chains, either to provide additional support for carrying big and bulky objects or to enable the dexterity that is required for in-hand manipulation. Since these complex systems often have a very high number of degrees of freedom coordinating their movements is notoriously difficult to model. In this article, we present the derivation of the theoretical foundations for cooperative task spaces of multi-arm robotic systems based on geometric primitives defined using conformal geometric algebra. Based on the similarity transformations of these cooperative geometric primitives, we derive an abstraction of complex robotic systems that enables representing these systems in a way that directly corresponds to single-arm systems. By deriving the associated analytic and geometric Jacobian matrices, we then show the straightforward integration of our approach into classical control techniques rooted in operational space control. We demonstrate this using bimanual manipulators, humanoids and multi-fingered hands in optimal control experiments for reaching desired geometric primitives and in teleoperation experiments using differential kinematics control. We then discuss how the geometric primitives naturally embed nullspace structures into the controllers that can be exploited for introducing secondary control objectives. This work, represents the theoretical foundations of this cooperative manipulation control framework, and thus the experiments are presented in an abstract way, while giving pointers towards potential future applications.
Recursive Forward Dynamics for Serial Kinematic Chains using Conformal Geometric Algebra

The computation of the forward dynamics plays an important role in simulating the motion of interconnected rigid bodies while considering the physical properties and constraints of each part. The applications in graphics, animation, and robotics usually require fast computation, which leads to the usage of fast recursive algorithms. In this paper, we present a formulation of the recursive forward dynamics of serial kinematic chains that that is rooted in geometry, which allows coordinate-free view and geometrically meaningful interpretations of the involved quantities. The mathematical framework is called conformal geometric algebra (CGA) and it extends classical vector algebra by introducing a unified representation of a large array of geometric operations, transformations and mathematical objects, such as points, lines, and planes, in a rigorous yet intuitive manner. Hence, using CGA for the computation of the forward dynamics provides a unified mathematical framework that seamlessly integrates both the geometric and dynamic aspects of the system. We validate the computation numerically and provide an implementation of the results in an open-source library, making it immediately available in practice.
Tactile Ergodic Control using Diffusion and Geometric Algbra
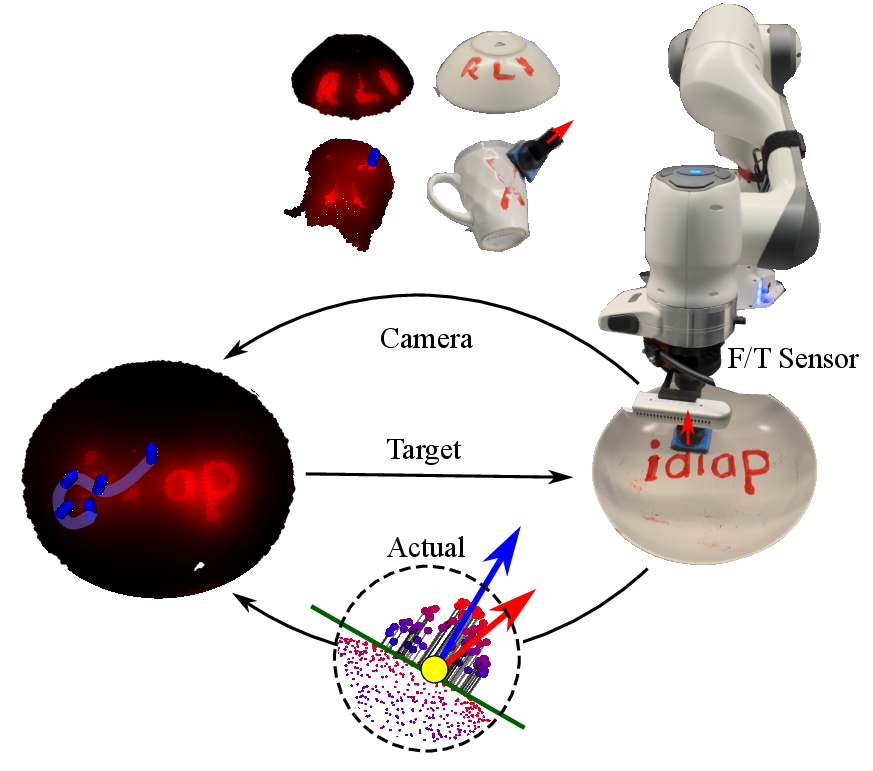
Continuous physical interaction between robots and their environment is a requirement in many industrial and household tasks, such as sanding and cleaning. Due to the complex tactile information, these tasks are notoriously difficult to model and to sense. Thus, planning open-loop trajectories is extremely challenging and likely to fail. In this article, we introduce a closed-loop control method that is constrained to surfaces. The applications that we target have in common that they can be represented by probability distributions on the surface that correlate to the time the robot should spend in a region. These surfaces can easily be captured jointly with the target distributions using coloured pointclouds. Hence, we present the extension of an ergodic control approach that can be used with pointclouds, based on heat equation-driven area coverage (HEDAC). Our method enables closed-loop exploration by measuring the actual coverage using vision. Unlike existing approaches, we approximate the potential field from non-stationary diffusion using spectral acceleration, which does not require complex preprocessing steps and achieves real-time closed-loop control frequencies. We exploit geometric algebra to stay in contact with the target surface by tracking a line while simultaneously exerting a desired force along that line, for which we are using a wrist-mounted force-torque sensor. Our approach is suitable for fully autonomous and human-robot interaction settings where the robot can either directly measure the coverage of the target with its sensors or by being guided online by markings or annotations of a human expert. We tested the performance of our approach in kinematic simulation using pointclouds, ranging from the Stanford bunny to a variety of kitchen utensils. Our real-world experiments demonstrate that the proposed approach can successfully be used to wash kitchenware with curved surfaces, by cleaning the dirt detected by vision in an online manner. We release all our source codes, experiment data and videos as open access at https://geometric-algebra.tobiloew.ch/tactile_ergodic_control/.
Extending the Cooperative Dual-Task Space in Conformal Geometric Algebra

In this work, we are presenting an extension of the cooperative dual-task space (CDTS) in conformal geometric algebra. The CDTS was first defined using dual quaternion algebra and is a well established framework for the simplified definition of tasks using two manipulators. By integrating conformal geometric algebra, we aim to further enhance the geometric expressiveness and thus simplify the modeling of various tasks. We show this formulation by first presenting the CDTS and then its extension that is based around a cooperative pointpair. This extension keeps all the benefits of the original formulation that is based on dual quaternions, but adds more tools for geometric modeling of the dual-arm tasks. We also present how this CGA-CDTS can be seamlessly integrated with an optimal control framework in geometric algebra that was derived in previous work. In the experiments, we demonstrate how to model different objectives and constraints using the CGA-CDTS. Using a setup of two Franka Emika robots we then show the effectiveness of our approach using model predictive control in real world experiments.
gafro: Geometric Algebra for Robotics
Geometry is a fundamental part of robotics and there have been various frameworks of representation over the years. Recently, geometric algebra has gained attention for its property of unifying many of those previous ideas into one algebra. While there are already efficient open-source implementations of geometric algebra available, none of them is targeted at robotics applications. We want to address this shortcoming with our library gafro. This article presents an overview of the implementation details as well as a tutorial of gafro, an efficient c++ library targeting robotics applications using geometric algebra. The library focuses on using conformal geometric algebra. Hence, various geometric primitives are available for computation as well as rigid body transformations. The modeling of robotic systems is also an important aspect of the library. It implements various algorithms for calculating the kinematics and dynamics of such systems as well as objectives for optimisation problems. The software stack is completed by python bindings in pygafro and a ROS interface in gafro_ros.
Geometric Algebra for Optimal Control with Application in Manipulation Tasks
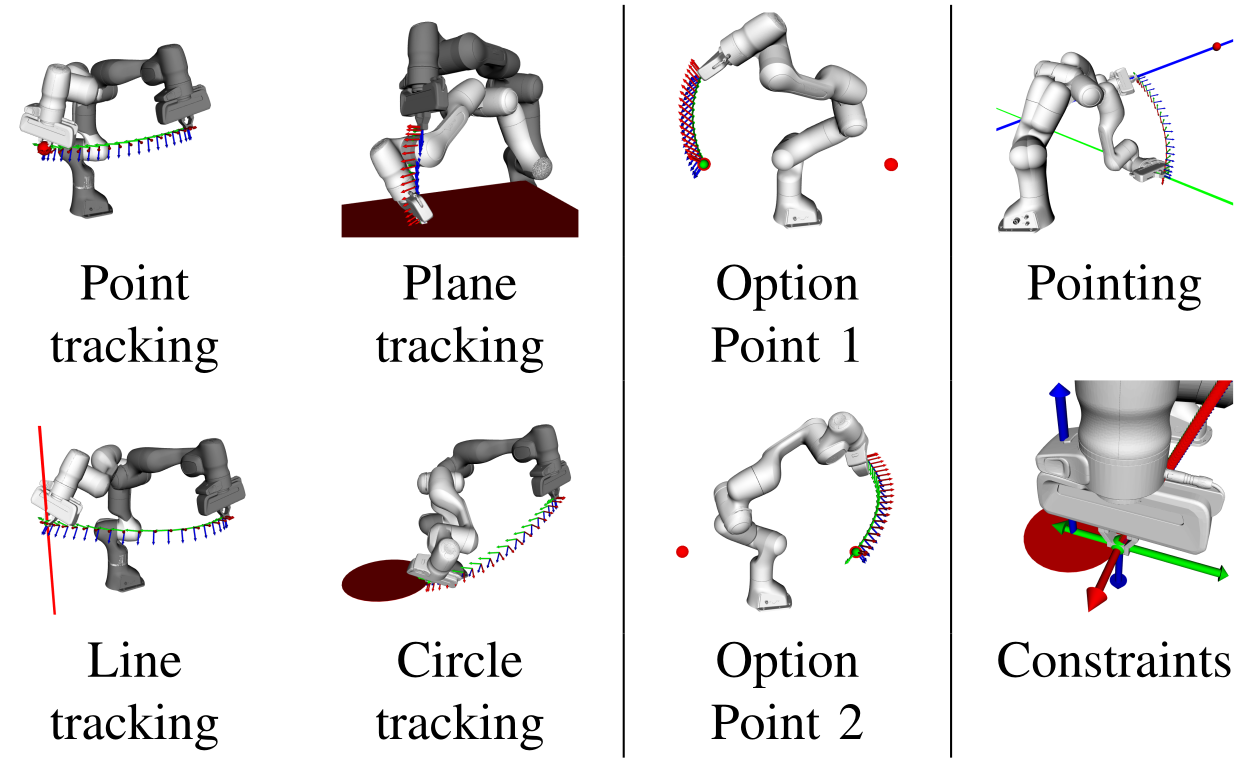
Many problems in robotics are fundamentally problems of geometry, which lead to an increased research effort in geometric methods for robotics in recent years. The results were algorithms using the various frameworks of screw theory, Lie algebra and dual quaternions. A unification and generalization of these popular formalisms can be found in geometric algebra. The aim of this paper is to showcase the capabilities of geometric algebra when applied to robot manipulation tasks. In particular the modelling of cost functions for optimal control can be done uniformly across different geometric primitives leading to a low symbolic complexity of the resulting expressions and a geometric intuitiveness. We demonstrate the usefulness, simplicity and computational efficiency of geometric algebra in several experiments using a Franka Emika robot. The presented algorithms were implemented in c++20 and resulted in the publicly available library gafro. The benchmark shows faster computation of the kinematics than state-of-the-art robotics libraries.